Rumus TRAPESIUM & Pengertiannya

 Trapesium adalah bangun dua dimensi bersisi empat dengan sisi sejajar dan panjang berbeda. Rumus untuk menghitung luas trapesium adalah L = ½(b1+b2)t, yaitu b1 dan b2 adalah panjang sisi-sisi sejajar dan t adalah tinggi.


pengertian trapesium

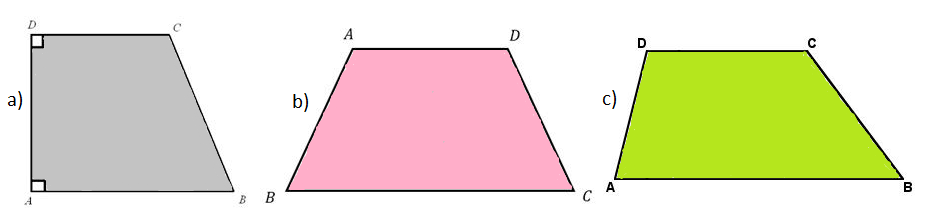
Kalau dilihat dari jenisnya, trapesium dibagi menjadi tiga jenis: trapesium siku-siku, sama kaki, dan tidak beraturan.

jenis trapesium
a) trapesium siku-siku, b) trapesium sama kaki, dan c) trapesium tidak beraturan

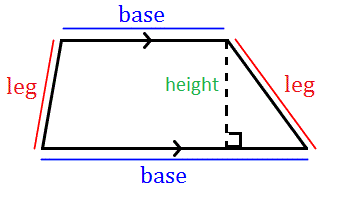
Berdasarkan gambar bangun trapesium di atas, maka dapat dipastikan bahwa trapesium memiliki luas dan keliling.

Luas trapesium = ½ x (alas a + alas b) x tinggi trapesium

Keliling trapesium = a + b + c + d (semua sisi ditambahkan)

Contoh Soal 1

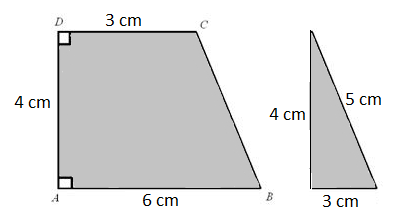
Sebuah trapesium memiliki panjang alas 3 cm dan 6 cm, kemudian tinggi dari trapesium tersebut adalah 4 cm. Berapa luas dan keliling bangun trapesium tersebut?

Pembahasan

contoh soal trapesium dan pembahasannya

Luas trapesium = ½ x (alas a + alas b) x tinggi trapesium 

                         = ½ x (3 + 6) x 4 = 18 cm persegi.

jadi luas trapesium adalah 18 cm2

Untuk mencari keliling trapesium, cari dulu sisi miringnya menggunakan phytagoras.

Keliling trapesium = a + b + c + d 

                                       = 3 + 4 + 6 + 5

                                       = 18 cm.

jadi keliling Trapesium adalah 18 cm

Contoh Soal 2

Terdapat sebuah trapesium dengan panjang sisi sejajar masing-masing 20 cm dan 12 cm serta tinggi 6 cm. Berapakah luas trapesium tersebut?

Solusi:

Dengan rumus yang sebelumnya sudah kita pelajari, maka

L = ½ × jumlah panjang sisi sejajar × tinggi

L = ½ × (20 + 12) × 6

L = ½ × 32 × 6

L = 96 cm²

———-

 

Komentar

  1. Migu Gunawan2 Juli 2021 pukul 08.49

    Bagaimana mencari tinggi jika luas trapesium belum diketahui

    BalasHapus
    Balasan
    1. indra_fassya_blog's13 Juli 2021 pukul 00.08

      Trimakasih @Migu Gunawan:
      Cara mencari tinggi trapesium apabila tidak diketahui Luasnya, tapi diketahui kedua sisinya yang sejajar serta sisi miring, maka bisa menggunakan Rumus Pythagoras

      Pada soal ini kita akan mempelajari tentang Teorema Pythagoras

      Bunyi Teorema Pythagoras adalah kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi penyikunya

      Contohnya :

      Pada sebuah segitiga siku-siku ABC

      Siku siku di B

      Maka AB dan BC adalah sisi penyikunya

      AC adalah sisi miring / Hipotenusa

      Maka berlaku perbandingan sisi :

      AC² = AB² + BC²

      Pembahasan :
      Diketahui :

      Trapesium siku-siku

      sisi-sisi sejajar = AB dan CD

      sisi miring = BC

      Ditanya :

      Tinggi ?

      Dijawab :

      Pertama-tama kita kurangkan dahulu sisi terpanjang dan terpendek agar mendapatkan salah satu sisi penyiku segitiga

      CE = x

      x = CD - AB

      Selanjutnya kita cari tinggi trapesium dengan rumus Pythagoras

      BC² = BE² + CE²

      BE² = BC² - CE²

      BE =

      ∴ Jadi tinggi trapesium = BE =

      Hapus

Posting Komentar

Postingan populer dari blog ini

Rumus Lingkaran & pengertiannya

Gambar
  Lingkaran adalah sebuah objek dua dimensi atau sebuah bidang  yang dibentuk oleh kumpulan titik yang mempunyai jarak yang sama dari titik pusat. Pada tengah-tengah lingkaran terdapat sebuah titik yang bernama  titik pusat lingkaran , titik pusat   Lingkaran  menjadi tolak ukur sebuah lingkaran dimana jarak antara titik pusat dengan titik terluar dari lingkaran disebut dengan  jari-jari lingkaran . Sedangkan jarak antar titik terluar yang melewati titik pusat disebut dengan  diameter lingkaran . Diameter dari sebuah lingkaran memiliki jarak dua kali jari-jari lingkaran   d = 2 x r Keterangan : r = jari-jari d = diameter Luas Lingkaran Luas lingkaran adalah ukuran seberapa besar daerah yang berada di dalam sebuah lingkaran. Untuk menghitung sebuah lingkaran diperlukan konstanta π “ phi ”. Definisi dari  phi  sendiri adalah sebuah konstanta dari perbandingan keliling lingkaran K dengan diameter d yang bernilai 22/7 atau biasa dibulatkan menjadi 3,14. π = K / d Rumus luas lingkaran diten
Baca selengkapnya

Rumus Belah ketupat & pengertiannya

Gambar
Belah Ketupat adalah bangun datar 2 dimensi yang dibentuk oleh 4 buah sisi yang sama panjang dan mempunyai 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan mempunyai besar sama.  Sifat-Sifat Belah Ketupat Keempat sisinya sama panjang Mempunyai 2 diagonal yang saling tegak lurus Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°). Sudut yang saling berhadapan mempunyai besar yang sama Pada belah ketupat sudut yang berhadapan mempunyai besar yang sama. Ilustrasi di atas menunjukkan besar sudut ∠ABC = ∠ADC dan ∠BAD = ∠BCD. Besar keempat titik sudutnya 360º Mempunyai 2 sumbu simetri yang merupakan diagonalnya  * Rumus Belah Ketupat Nama Rumus Keliling (Kll) Kll = s + s + s + s Kll = s × 4 Luas (L) L = ½ × d1 × d2 Sisi (s) s = Kll ÷ 4 Diagonal 1 (d1) d1 = 2 × L ÷ d2 Diagonal 2 (d2) d2 = 2 × L ÷ d1    Contoh 1: Menggunakan Rumus Keliling Belah Ketupat Hitunglah keliling belah ketupat yang mempunyai panjang sisi 7 cm! Dik
Baca selengkapnya